The Case of the Zachary Karate Club Network
Graphs are a powerful way to represent and analyze relationships between entities. In graph theory, a graph is made up of nodes (also called vertices) and edges (the connections between nodes). This structure allows us to model anything from social networks to biological systems, transportation routes, or internet links. When data naturally forms a network of relationships, we call it graph-structured data.
Let’s consider a concrete example: the Zachary Karate Club Network. In the 1970s, Wayne Zachary, an American anthropologist, studied the social interactions between 34 members of a university karate club(1). Over two years, he recorded who interacted with whom outside of formal classes. The resulting data formed a graph, where each member of the club is represented as a node, and an edge exists between two members if they had social interactions.
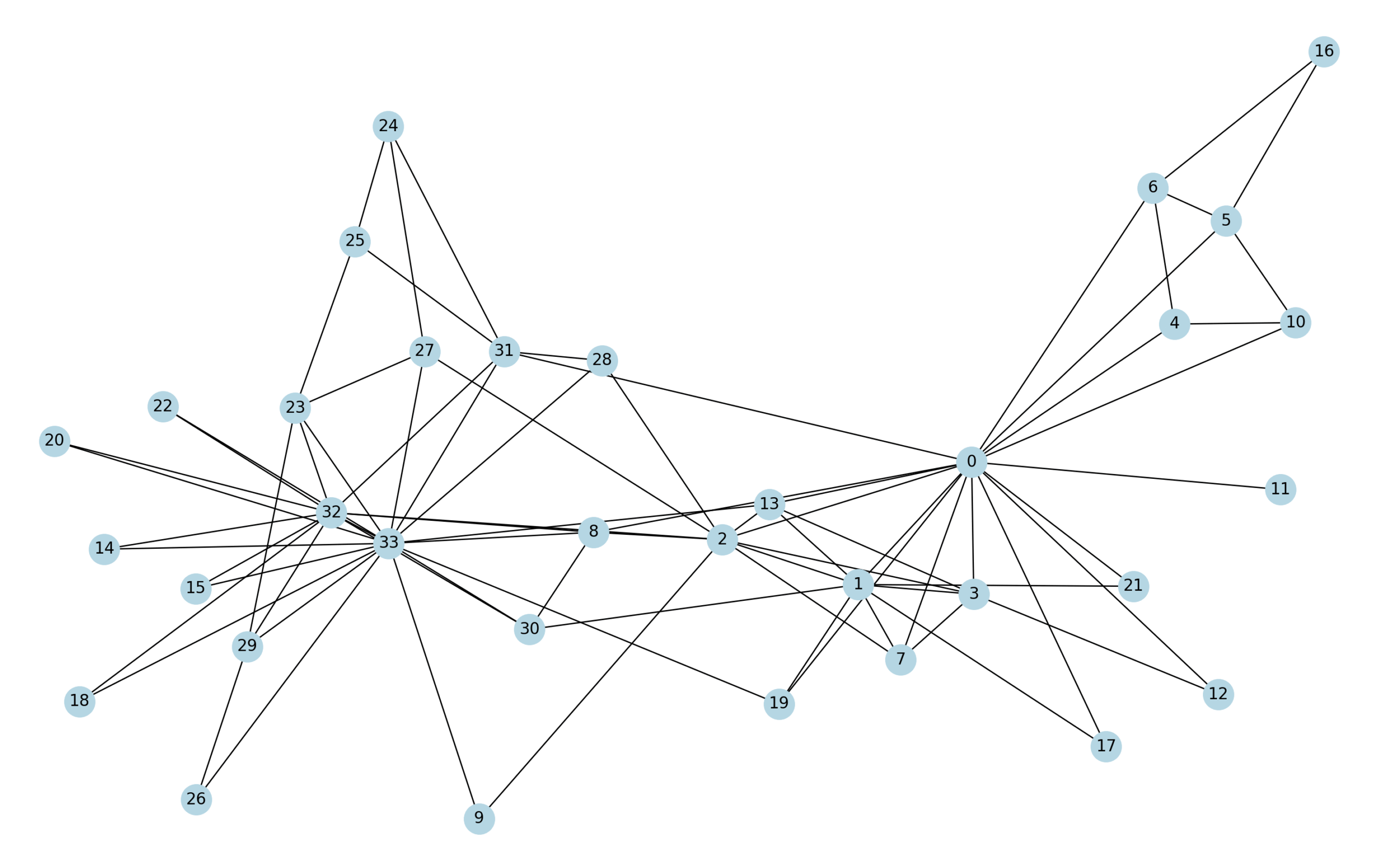
This network is more than just a set of friendships. It reveals patterns of social structure. For example, some individuals are more connected than others—they have more edges linking them to other nodes. In graph theory, this is called a node’s degree. A person with a high degree might be a popular or central figure in the club. In the Zachary Karate Club, the instructor (node 0) and the club president (node 33) had the highest degrees, indicating they were important social hubs.
Graph-structured data also allows us to detect communities—groups of nodes that are more densely connected internally than with the rest of the network. In fact, one of the most famous aspects of this dataset is that, during Zachary’s study, the club split into two factions following a dispute between the instructor and the president. Members had to choose sides: some stayed with the instructor, while others left to form a new club under the president. This real-world split was reflected in the structure of the network, with most members aligning themselves with the leader to whom they were more closely connected.
Graph analysis can predict such splits using algorithms like community detection or network partitioning. Remarkably, algorithms applied to the Zachary Karate Club network were able to predict the eventual division with high accuracy, based solely on the patterns of connections before the split occurred.
Beyond identifying communities, graph analysis lets us explore concepts like centrality (who is most influential?), shortest paths (how closely connected are two individuals?), and network robustness (how does the network behave if key nodes are removed?). Each of these insights is valuable in fields as diverse as sociology, epidemiology, computer science, and business.
The Zachary Karate Club Network remains a classic example because it is small enough to visualize and analyze manually, yet rich enough to illustrate key concepts in graph theory. By studying it, we learn how a simple representation of relationships—a graph—can reveal the underlying dynamics of a social system.